Difference between revisions of "Week4a"
(Created page with "== Activities == '''Activity 1.''' Below is the graph of a function f: Rocket's velocity versus time Compute the following limits. Note t...") |
|||
| (2 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | == Activities == | + | <div class="toccolours mw-collapsible mw-collapsed" style="width:1000px"> |
| + | ===Activities=== | ||
| + | <div class="mw-collapsible-content"> | ||
| − | '''Activity | + | '''Activity: interpreting limits from a graph.''' |
Below is the graph of a function f: | Below is the graph of a function f: | ||
| Line 50: | Line 52: | ||
u) $\lim_{x\rightarrow 0} f(\cos{x})$ | u) $\lim_{x\rightarrow 0} f(\cos{x})$ | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <div class="toccolours mw-collapsible mw-collapsed" style="width:1000px"> | ||
| + | ===Clicker Questions=== | ||
| + | <div class="mw-collapsible-content"> | ||
| + | |||
| + | '''Question.''' | ||
| + | |||
| + | The statement, “Whether or not $\lim_{x\rightarrow a} f(x)$ exists depends on how $f(a)$ is defined,” is true | ||
| + | |||
| + | a) Never. | ||
| + | |||
| + | b) Sometimes. | ||
| + | |||
| + | c) Always. | ||
| + | |||
| + | |||
| + | '''Question.''' | ||
| + | |||
| + | If a function $f$ is not defined at $x=a$, then | ||
| + | |||
| + | a) $\lim_{x\rightarrow a} f(x)$ cannot exist. | ||
| + | |||
| + | b) $\lim_{x\rightarrow a} f(x)$ could be 2. | ||
| + | |||
| + | c) $\lim_{x\rightarrow a} f(x)$ must approach infinity. | ||
| + | |||
| + | d) Not enough information. | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
Latest revision as of 15:46, 3 November 2014
Activities
Activity: interpreting limits from a graph.
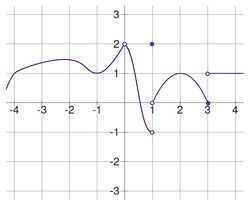
Below is the graph of a function f:
Compute the following limits. Note that some of your answers will only be approximate.
a) $f(0)$
b) $f(1.5)$
c) $f(1)$
d) $f(0.9)$
e) $f(1.1)$
f) $\lim_{x\rightarrow 1^+} f(x)$
g) $\lim_{x\rightarrow 1^-} f(x)$
h) $\lim_{x\rightarrow 1} f(x)$
i) $f(1.9)$
j) $f(2.1)$
k) $\lim_{x\rightarrow 2} f(x)$
l) $f(f(1.9))$
m) $f(f(2.1))$
n) $\lim_{x\rightarrow 2^+} f(f(x))$
o) $\lim_{x\rightarrow 2^-} f(f(x))$
p) $\lim_{x\rightarrow 2} f(f(x))$
q) $\lim_{x\rightarrow -1} f(f(x))$
r) $\lim_{x\rightarrow 4} f(f(x))$
s) $\lim_{x\rightarrow -4} f(f(x))$
t) $\lim_{x\rightarrow 0} f(1+x^2)$
u) $\lim_{x\rightarrow 0} f(\cos{x})$
Clicker Questions
Question.
The statement, “Whether or not $\lim_{x\rightarrow a} f(x)$ exists depends on how $f(a)$ is defined,” is true
a) Never.
b) Sometimes.
c) Always.
Question.
If a function $f$ is not defined at $x=a$, then
a) $\lim_{x\rightarrow a} f(x)$ cannot exist.
b) $\lim_{x\rightarrow a} f(x)$ could be 2.
c) $\lim_{x\rightarrow a} f(x)$ must approach infinity.
d) Not enough information.