Difference between revisions of "Week2a"
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | [[Media:Quadratic-fns.pdf|Handout on quadratic functions]] | + | <div class="toccolours mw-collapsible mw-collapsed" style="width:1000px"> |
| − | + | ===Handouts=== | |
| + | <div class="mw-collapsible-content"> | ||
| + | *[[Media:Linear-fns.pdf|Handout on linear functions]] | ||
| + | *[[Media:Quadratic-fns.pdf|Handout on quadratic functions]] | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| − | |||
| + | <div class="toccolours mw-collapsible mw-collapsed" style="width:1000px"> | ||
| + | === Activities === | ||
| + | <div class="mw-collapsible-content"> | ||
'''Activity: working with linear functions.''' | '''Activity: working with linear functions.''' | ||
| Line 35: | Line 41: | ||
b) Suppose $f$ is even and $g$ is odd. Evaluate $f(-3)$ and $g(-5)$. | b) Suppose $f$ is even and $g$ is odd. Evaluate $f(-3)$ and $g(-5)$. | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
| − | == Extra discussion questions == | + | <div class="toccolours mw-collapsible mw-collapsed" style="width:1000px"> |
| + | === Extra discussion questions === | ||
| + | <div class="mw-collapsible-content"> | ||
# Find a constant $k$ such that the line through the points $(k,2)$ and $(3,6)$ has the same rate of change as the line $y=4x+3$. | # Find a constant $k$ such that the line through the points $(k,2)$ and $(3,6)$ has the same rate of change as the line $y=4x+3$. | ||
| Line 44: | Line 55: | ||
# Find the number $c$ such that $x^2+5x+c$ is a perfect square for all $x$ values. | # Find the number $c$ such that $x^2+5x+c$ is a perfect square for all $x$ values. | ||
# Determine the $x$-values for which $x^2+4x+1\geq 1$. How would you solve this graphically? | # Determine the $x$-values for which $x^2+4x+1\geq 1$. How would you solve this graphically? | ||
| + | </div> | ||
| + | </div> | ||
Revision as of 15:43, 3 November 2014
Activities
Activity: working with linear functions.
The temperature scales Celsius and Fahrenheit have a linear relationship with $0^{\circ}C = 32^{\circ}F$ and $100^{\circ}C = 212^{\circ}F$.
- Write a linear equation expressing $F$ in terms of $C$ and sketch its graph.
- If it is $75^{\circ}C$, what is the temperature in $F$?
- If it is $75^{\circ}F$, what is the temperature in $C$?
- What about if it is $175^{\circ}F$?
- What about if it is $-25^{\circ}F$?
- Did you compute each $C$ in parts (3) - (5) separately? Could you have avoided this?
- Graph the line $F=C$ on the same axes. Can you tell from your graph if there a temperature $x$ for which $x^{\circ}C=x^{\circ}F$? If so, what is $x$?
Activity: working with quadratic functions.
The revenue of Miley Cyrus' concert in Vancouver depends on the number of unsold seats. Miley's manager calculates that the revenue is given by $R(x) = 8000+70x-x^2$, where $x$ is the number of unsold seats. Find the maximum revenue and the number of unsold seats that corresponds to maximum revenue.
Activity: working with general functions.
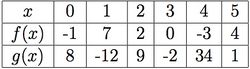
Consider the following table of function values for $f(x)$ and $g(x)$.
a) Evaluate: $(f+g)(4)$, $\dfrac{f}{g}(3)$, $\dfrac{g}{f}(3)$, $(f\cdot g)(5)$, $(f\circ g)(5)$, $(g\circ f)(2)$, $f^{-1}(-3)$, $g^{-1}(8)$.
b) Suppose $f$ is even and $g$ is odd. Evaluate $f(-3)$ and $g(-5)$.
Extra discussion questions
- Find a constant $k$ such that the line through the points $(k,2)$ and $(3,6)$ has the same rate of change as the line $y=4x+3$.
- Graphically determine the $x$-values for which $\frac{2}{5}x+7>3$.
- Suppose that a bar charges a $\$8$ cover fee upon entry and $\$4.75$ per drink. Write a linear equation representing your cost for a night out in terms of how many drinks you ordered.
- Find the number $c$ such that $x^2+5x+c$ is a perfect square for all $x$ values.
- Determine the $x$-values for which $x^2+4x+1\geq 1$. How would you solve this graphically?