Week2a
Contents |
Handouts
Activities
Activity: working with linear functions.
The temperature scales Celsius and Fahrenheit have a linear relationship with $0^{\circ}C = 32^{\circ}F$ and $100^{\circ}C = 212^{\circ}F$.
- Write a linear equation expressing $F$ in terms of $C$ and sketch its graph.
- If it is $75^{\circ}C$, what is the temperature in $F$?
- If it is $75^{\circ}F$, what is the temperature in $C$?
- What about if it is $175^{\circ}F$?
- What about if it is $-25^{\circ}F$?
- Did you compute each $C$ in parts (3) - (5) separately? Could you have avoided this?
- Graph the line $F=C$ on the same axes. Can you tell from your graph if there a temperature $x$ for which $x^{\circ}C=x^{\circ}F$? If so, what is $x$?
Activity: working with quadratic functions.
The revenue of Miley Cyrus' concert in Vancouver depends on the number of unsold seats. Miley's manager calculates that the revenue is given by $R(x) = 8000+70x-x^2$, where $x$ is the number of unsold seats. Find the maximum revenue and the number of unsold seats that corresponds to maximum revenue.
Activity: working with general functions.
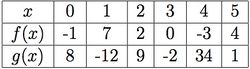
Consider the following table of function values for $f(x)$ and $g(x)$.
a) Evaluate: $(f+g)(4)$, $\dfrac{f}{g}(3)$, $\dfrac{g}{f}(3)$, $(f\cdot g)(5)$, $(f\circ g)(5)$, $(g\circ f)(2)$, $f^{-1}(-3)$, $g^{-1}(8)$.
b) Suppose $f$ is even and $g$ is odd. Evaluate $f(-3)$ and $g(-5)$.
Clicker Questions
Question.
What is the domain of $f(x)=\sqrt{x-5}$?
a) $x\geq 5$.
b) $x> 5$.
c) $x\neq 5$.
d) All real numbers.
Question.
What is the domain of $f(x)=\dfrac{2x}{\sqrt{x-5}}$?
a) $x\geq 5$.
b) $x> 5$.
c) $x\neq 5$.
d) All real numbers.
Question.
Which of the following functions has its domain equal to its range?
a) $f(x)=x^2$.
b) $g(x)=\sqrt{x}$.
c) $h(x)=|x|$.
d) All functions have that property.
Question.
What is the slope of a line passing through the points $(1,4)$ and $(3,8)$?
a) $1/2$.
b) $-1/2$.
c) $2$.
d) $-2$.
Question.
Which of the following lines has a different slope than all the others?
a) $6x-2y+7=0$.
b) $y=3x-1$.
c) $3y=3x-4$.
d) $9x=3y+3$.
Question.
What is the average rate of change of $f(t)=t^2$ between $t=1$ an $t=3$?
a) 1/8.
b) 1/4.
c) 4.
d) 8.
Question.
Consider the following table of function values for $f(x)$ and $g(x)$.
What is $f(g(5))$?
a) 4.
b) 7.
c) 34.
d) Cannot be determined.
Question.
Consider the following table of function values for $f(x)$ and $g(x)$.
If $g(f(x))=9$, then what is $x$?
a) 0.
b) 1.
c) 2.
d) Cannot be determined.
Question.
Consider the following table of function values for $f(x)$ and $g(x)$.
What is $f(g(5))$?
a) 4.
b) 7.
c) 34.
d) Cannot be determined.
Extra discussion questions
- Find a constant $k$ such that the line through the points $(k,2)$ and $(3,6)$ has the same rate of change as the line $y=4x+3$.
- Graphically determine the $x$-values for which $\frac{2}{5}x+7>3$.
- Suppose that a bar charges a $\$8$ cover fee upon entry and $\$4.75$ per drink. Write a linear equation representing your cost for a night out in terms of how many drinks you ordered.
- Find the number $c$ such that $x^2+5x+c$ is a perfect square for all $x$ values.
- Determine the $x$-values for which $x^2+4x+1\geq 1$. How would you solve this graphically?