Difference between revisions of "Tutorial Week 6"
From UBCMATH WIKI
(Created page with "===Worksheet Questions, February 23, 2015 === #Salt water with concentration of 1 g/L flows into Tank A at a rate $a$ L/min. The mixed solution in Tank A flows into Tank B at...") |
|||
| Line 1: | Line 1: | ||
| − | ===Worksheet Questions, February | + | ===Worksheet Questions, February 22, 2016 === |
#Salt water with concentration of 1 g/L flows into Tank A at a rate $a$ L/min. The mixed solution in Tank A flows into Tank B at a rate $b$ L/min. Another pipe takes the solution in Tank B back into Tank A at a rate $c$ L/min. Finally, solution drains out of Tank B at a rate $a$ L/min. '''Note''': the volume in each tank is the same and $a$+$c$=$b$ (to ensure that the volumes in the tanks are constant). | #Salt water with concentration of 1 g/L flows into Tank A at a rate $a$ L/min. The mixed solution in Tank A flows into Tank B at a rate $b$ L/min. Another pipe takes the solution in Tank B back into Tank A at a rate $c$ L/min. Finally, solution drains out of Tank B at a rate $a$ L/min. '''Note''': the volume in each tank is the same and $a$+$c$=$b$ (to ensure that the volumes in the tanks are constant). | ||
## Write down the system that gives the amount of salt in each tank at any given time. | ## Write down the system that gives the amount of salt in each tank at any given time. | ||
## Show that it is impossible for this system to have oscillations (damped or otherwise). | ## Show that it is impossible for this system to have oscillations (damped or otherwise). | ||
| − | #Plot the phase plane for the following | + | #Plot the phase plane for the following systems of equations. Your phase plane should include eigen-directions for real eigenvalues and several solutions illustrating the general shapes of solutions in the phase plane. |
| − | \begin{eqnarray} | + | ##\begin{eqnarray} |
| − | x_1 &=& x_1 -8x_2 \\ | + | x_1' &=& x_1 -8x_2 \\ |
| − | x_2 &=& 8x_1+x_2 | + | x_2' &=& 8x_1+x_2 |
| + | \end{eqnarray} | ||
| + | ##\begin{eqnarray} | ||
| + | x_1' &=& x_2 \\ | ||
| + | x_2' &=& -3x_1-4x_2 | ||
\end{eqnarray} | \end{eqnarray} | ||
===Solutions:=== | ===Solutions:=== | ||
| − | # | + | #('''6pts'''+'''2pts''') |
##\begin{eqnarray} | ##\begin{eqnarray} | ||
Q_1^\prime &=& (1)\cdot a -b\frac{Q_1}{V} + c\frac{Q_2}{V} \\ | Q_1^\prime &=& (1)\cdot a -b\frac{Q_1}{V} + c\frac{Q_2}{V} \\ | ||
Q_2^\prime &=& b\frac{Q_1}{V} -(a+c)\frac{Q_2}{V} | Q_2^\prime &=& b\frac{Q_1}{V} -(a+c)\frac{Q_2}{V} | ||
| − | \end{eqnarray} | + | \end{eqnarray} For each equation, '''1 pt''' for form (positive and negative terns in a DE), '''2 pts''' for the details of the terms (Q, V) so total '''6 pts'''. |
| − | ## Eigenvalues of the homogeneous equation are: $-b \pm \sqrt{bc}$. Since b,c $\ge$ 0, the eigenvalues are real and the system can not have oscillations. | + | ## Eigenvalues of the homogeneous equation are: $-b \pm \sqrt{bc}$ '''(1 pt)'''. Since b,c $\ge$ 0, the eigenvalues are real and the system can not have oscillations ('''1 pt''' - must state this explicitly). |
| − | # | + | #('''3pts'''+'''6pts''') |
| + | ##'''1 pt''' for eigenvalues (1+ 8i & 1-8i) , '''1 pt''' for growing spiral, '''1 pt''' for direction of rotation (must have some justification for choice) | ||
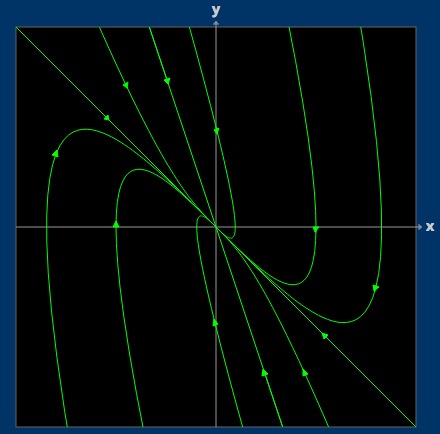
| + | ##'''1 pt''' for eigenvalues (-1& -3), '''2 pts''' for eigenvectors (e.g. (-1,1) for -1, and (-1, 3) for -3), '''3 pts''' for drawing ('''1 pt''' for including a solution in each of the two eigen-directions with arrows correct, '''1 pt''' for shape of non-eigen solutions, '''1 pt''' for direction of arrows on non-eigen solutions). | ||
| + | Here are example answers to these two questions. The vector fields are not necessary but there should be arrows showing direction along the eigen-directions and the solution curves. | ||
| + | https://www.desmos.com/calculator/oy3oslqfya | ||
| + | https://www.desmos.com/calculator/60djgxc0hn (Drag the blue point to see different solution curves.) | ||
| + | [[File:Question 2b.jpeg]] | ||
Revision as of 11:17, 29 February 2016
Worksheet Questions, February 22, 2016
- Salt water with concentration of 1 g/L flows into Tank A at a rate $a$ L/min. The mixed solution in Tank A flows into Tank B at a rate $b$ L/min. Another pipe takes the solution in Tank B back into Tank A at a rate $c$ L/min. Finally, solution drains out of Tank B at a rate $a$ L/min. Note: the volume in each tank is the same and $a$+$c$=$b$ (to ensure that the volumes in the tanks are constant).
- Write down the system that gives the amount of salt in each tank at any given time.
- Show that it is impossible for this system to have oscillations (damped or otherwise).
- Plot the phase plane for the following systems of equations. Your phase plane should include eigen-directions for real eigenvalues and several solutions illustrating the general shapes of solutions in the phase plane.
- \begin{eqnarray} x_1' &=& x_1 -8x_2 \\ x_2' &=& 8x_1+x_2 \end{eqnarray}
- \begin{eqnarray} x_1' &=& x_2 \\ x_2' &=& -3x_1-4x_2 \end{eqnarray}
Solutions:
- (6pts+2pts)
- \begin{eqnarray} Q_1^\prime &=& (1)\cdot a -b\frac{Q_1}{V} + c\frac{Q_2}{V} \\ Q_2^\prime &=& b\frac{Q_1}{V} -(a+c)\frac{Q_2}{V} \end{eqnarray} For each equation, 1 pt for form (positive and negative terns in a DE), 2 pts for the details of the terms (Q, V) so total 6 pts.
- Eigenvalues of the homogeneous equation are: $-b \pm \sqrt{bc}$ (1 pt). Since b,c $\ge$ 0, the eigenvalues are real and the system can not have oscillations (1 pt - must state this explicitly).
- (3pts+6pts)
- 1 pt for eigenvalues (1+ 8i & 1-8i) , 1 pt for growing spiral, 1 pt for direction of rotation (must have some justification for choice)
- 1 pt for eigenvalues (-1& -3), 2 pts for eigenvectors (e.g. (-1,1) for -1, and (-1, 3) for -3), 3 pts for drawing (1 pt for including a solution in each of the two eigen-directions with arrows correct, 1 pt for shape of non-eigen solutions, 1 pt for direction of arrows on non-eigen solutions).
Here are example answers to these two questions. The vector fields are not necessary but there should be arrows showing direction along the eigen-directions and the solution curves.
https://www.desmos.com/calculator/oy3oslqfya https://www.desmos.com/calculator/60djgxc0hn (Drag the blue point to see different solution curves.)