Difference between revisions of "Exam review questions"
From UBCMATH WIKI
(Created page with "<ol> <li>How many distinct possibilities are there for $\lim_{t\to\infty}x(t)$ where $x(t)$ solves the equation $x'-x=e^t$? <ol> <li>1</li> <li> 2</li> ...") |
|||
| (2 intermediate revisions by one user not shown) | |||
| Line 8: | Line 8: | ||
</ol> | </ol> | ||
</li> | </li> | ||
| − | + | <br><br><br><br><br><br> | |
<li>Find the solution to the equation $y'=-x/y$ with the initial condition $y(0)=-2$. | <li>Find the solution to the equation $y'=-x/y$ with the initial condition $y(0)=-2$. | ||
<ol> | <ol> | ||
| Line 17: | Line 17: | ||
</ol> | </ol> | ||
</li> | </li> | ||
| − | + | <br><br><br><br><br><br> | |
<li> To solve the equation $y''+16\pi^2 y=f(t)$ using the Method of Undetermined Coefficients where $f(t)$ is a periodic function with period $T$ and $2T$ is not an integer, your guess at the particular solution should be | <li> To solve the equation $y''+16\pi^2 y=f(t)$ using the Method of Undetermined Coefficients where $f(t)$ is a periodic function with period $T$ and $2T$ is not an integer, your guess at the particular solution should be | ||
<ol> | <ol> | ||
| Line 26: | Line 26: | ||
</ol> | </ol> | ||
</li> | </li> | ||
| − | + | <br><br><br><br><br><br> | |
<li> The solution to the equation $y''+81y=f(t)$ where $f(t)$ is a switching function that continually goes on ($f(t)=1$) for one second and off ($f(t)=0$) for 1 second repeatedly. The solution consists of many sinusoidal functions but the one with largest amplitude has a period of | <li> The solution to the equation $y''+81y=f(t)$ where $f(t)$ is a switching function that continually goes on ($f(t)=1$) for one second and off ($f(t)=0$) for 1 second repeatedly. The solution consists of many sinusoidal functions but the one with largest amplitude has a period of | ||
<ol> | <ol> | ||
| Line 35: | Line 35: | ||
</ol> | </ol> | ||
</li> | </li> | ||
| − | + | <br><br><br><br><br><br> | |
<li> Consider the matrix equation $x'=Ax$ where $A=\begin{pmatrix} a & 3 \\ 1 & a \end{pmatrix}$. As the value of $a$ increases smoothly from a large negative number to a large positive number, the classification of the steady state... | <li> Consider the matrix equation $x'=Ax$ where $A=\begin{pmatrix} a & 3 \\ 1 & a \end{pmatrix}$. As the value of $a$ increases smoothly from a large negative number to a large positive number, the classification of the steady state... | ||
<ol> | <ol> | ||
| Line 44: | Line 44: | ||
</ol> | </ol> | ||
</li> | </li> | ||
| − | + | <br><br><br><br><br><br> | |
<li> The inverse transform of the function $\displaystyle Y(s)=\frac{s+3}{(s+1)^2+4}$ is | <li> The inverse transform of the function $\displaystyle Y(s)=\frac{s+3}{(s+1)^2+4}$ is | ||
<ol> | <ol> | ||
| Line 53: | Line 53: | ||
</ol> | </ol> | ||
</li> | </li> | ||
| − | + | <br><br><br><br><br><br> | |
<li> Which of the following are the eigenfunctions for the diffusion equation $u_t=16u_{xx}$ with boundary conditions $u(0,t)=0$ and $u_x(4,t)=0$? | <li> Which of the following are the eigenfunctions for the diffusion equation $u_t=16u_{xx}$ with boundary conditions $u(0,t)=0$ and $u_x(4,t)=0$? | ||
<ol> | <ol> | ||
| Line 62: | Line 62: | ||
</ol> | </ol> | ||
</li> | </li> | ||
| − | + | <br><br><br><br><br><br> | |
<li> Which of the following functions would be the correct choice for extending $f(x)$ in order to solve the diffusion equation on the interval $[0,1]$ with initial condition $f(x)=x$ and boundary conditions $u_x(0,t)=0$ and $u(1,t)=0$? | <li> Which of the following functions would be the correct choice for extending $f(x)$ in order to solve the diffusion equation on the interval $[0,1]$ with initial condition $f(x)=x$ and boundary conditions $u_x(0,t)=0$ and $u(1,t)=0$? | ||
| − | + | <br> | |
| − | + | (a) [[File:extendedFunction1.png|200px|a]] . . (b) [[File:extendedFunction2.png|200px|b]]<br><br> | |
| − | + | (c) [[File:extendedFunction3.png|200px|c]] . . (d) [[File:extendedFunction4.png|200px|d]] | |
| − | + | ||
| − | + | ||
| − | + | ||
</li> | </li> | ||
| − | + | <br><br><br><br><br><br> | |
<li> You add 5 grams of salt per minute through the left end ($x=0$) of a 3m pipe filled with water. The salt diffuses in the pipe with diffusion coefficient $D=2$ m$^2/$min. The right end of the pipe ($x=3$) is connected to an extremely large tank that starts with no salt in it. What is the steady state concentration profile through the pipe? | <li> You add 5 grams of salt per minute through the left end ($x=0$) of a 3m pipe filled with water. The salt diffuses in the pipe with diffusion coefficient $D=2$ m$^2/$min. The right end of the pipe ($x=3$) is connected to an extremely large tank that starts with no salt in it. What is the steady state concentration profile through the pipe? | ||
<ol> | <ol> | ||
| Line 80: | Line 77: | ||
</ol> | </ol> | ||
</li> | </li> | ||
| − | + | <br><br><br><br><br><br> | |
<li> Choose the best option for a guess at the particular solution to the equation $y'''+2y'' = t + e^{-2t}$. | <li> Choose the best option for a guess at the particular solution to the equation $y'''+2y'' = t + e^{-2t}$. | ||
<ol> | <ol> | ||
| Line 89: | Line 86: | ||
</ol> | </ol> | ||
</li> | </li> | ||
| − | + | <br><br><br><br><br><br> | |
<li> Books are taken out of a library at a constant rate. Books are returned to the library at a rate proportional to how many books are currently checked out from the library. On the 8th day of the semester, a large delivery of new books arrives at the library. Choose the best model for the number of books in the library $B(t)$ at time $t$ measured in days from the start of the semester. | <li> Books are taken out of a library at a constant rate. Books are returned to the library at a rate proportional to how many books are currently checked out from the library. On the 8th day of the semester, a large delivery of new books arrives at the library. Choose the best model for the number of books in the library $B(t)$ at time $t$ measured in days from the start of the semester. | ||
<ol> | <ol> | ||
| Line 98: | Line 95: | ||
</ol> | </ol> | ||
</li> | </li> | ||
| − | + | <br><br><br><br><br><br> | |
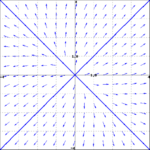
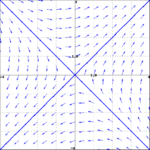
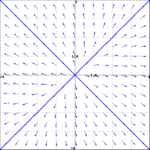
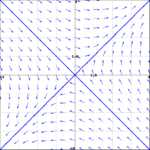
<li> Match the general solution to the vector field | <li> Match the general solution to the vector field | ||
<ol> | <ol> | ||
| Line 106: | Line 103: | ||
</ol> | </ol> | ||
</ol> | </ol> | ||
| − | + | (i) [[File:vectorfield1.png|150px|A]] (ii) [[File:vectorfield3.png|150px|B]] | |
| − | + | (iii) [[File:vectorfield4.png|150px|C]] (iv) [[File:vectorfield6.png|150px|D]] | |
| − | + | ||
| − | + | ||
| − | + | ||
<ol> | <ol> | ||
<li> (i) -- A; (ii) -- B.</li> | <li> (i) -- A; (ii) -- B.</li> | ||
Latest revision as of 13:01, 6 April 2017
- How many distinct possibilities are there for $\lim_{t\to\infty}x(t)$ where $x(t)$ solves the equation $x'-x=e^t$?
- 1
- 2
- 3
- 4
- Find the solution to the equation $y'=-x/y$ with the initial condition $y(0)=-2$.
- $y=\sqrt{-4-x^2}$
- $y=\sqrt{4-x^2}$
- $y=-\sqrt{4-x^2}$
- $x^2+y^2=4$
- To solve the equation $y''+16\pi^2 y=f(t)$ using the Method of Undetermined Coefficients where $f(t)$ is a periodic function with period $T$ and $2T$ is not an integer, your guess at the particular solution should be
- $y_p(t)=A \sin(4 \pi t) + B \cos(4\pi t)$
- $y_p(t)=A_0 + \sum_{n=1}^\infty a_n\cos\left(\frac{n \pi}{T} t\right) + \sum_{n=1}^\infty b_n\sin\left(\frac{n \pi}{T} t\right)$
- $y_p(t)=A_0 + \sum_{n=1}^\infty a_n\cos\left(\frac{2n \pi}{T} t\right) + \sum_{n=1}^\infty b_n\sin\left(\frac{2n \pi}{T} t\right)$
- $y_p(t)=A_0 + \sum_{n=1}^\infty a_n\cos\left(\frac{2n \pi}{T} t\right)$
- The solution to the equation $y''+81y=f(t)$ where $f(t)$ is a switching function that continually goes on ($f(t)=1$) for one second and off ($f(t)=0$) for 1 second repeatedly. The solution consists of many sinusoidal functions but the one with largest amplitude has a period of
- $\omega = \pi$
- $\omega = 2\pi$
- $\omega = 3\pi$
- $\omega = 4\pi$
- Consider the matrix equation $x'=Ax$ where $A=\begin{pmatrix} a & 3 \\ 1 & a \end{pmatrix}$. As the value of $a$ increases smoothly from a large negative number to a large positive number, the classification of the steady state...
- ... changes from a stable node to a stable spiral to an unstable spiral to an unstable node.
- ... is always a saddle.
- ... changes from a stable node to a saddle to an unstable node.
- ... changes from an unstable node to a saddle to a stable node.
- The inverse transform of the function $\displaystyle Y(s)=\frac{s+3}{(s+1)^2+4}$ is
- $\sqrt{2}e^{-t}\cos\left(2\left(t-\frac{\pi}{8}\right)\right)$
- $\sqrt{2}e^{-t}\cos\left(2\left(t-\frac{\pi}{4}\right)\right)$
- $\sqrt{2}e^{-t}\sin\left(2\left(t-\frac{\pi}{8}\right)\right)$
- $\sqrt{2}e^{-t}\cos\left(2\left(t+\frac{\pi}{4}\right)\right)$
- Which of the following are the eigenfunctions for the diffusion equation $u_t=16u_{xx}$ with boundary conditions $u(0,t)=0$ and $u_x(4,t)=0$?
- $\displaystyle u_n(x,t)=e^{-\frac{n^2\pi^2}{4}t} \sin\left( \frac{n\pi x}{8} \right)$ for $n$ even.
- $\displaystyle u_n(x,t)=e^{-n^2\pi^2t} \sin\left( \frac{n\pi x}{4} \right)$ for $n$ even.
- $\displaystyle u_n(x,t)=e^{-\frac{n^2\pi^2}{4}t} \sin\left( \frac{n\pi x}{8} \right)$ for $n$ odd.
- $\displaystyle u_n(x,t)=e^{-n^2\pi^2t} \sin\left( \frac{n\pi x}{4} \right)$ for $n$ odd.
- Which of the following functions would be the correct choice for extending $f(x)$ in order to solve the diffusion equation on the interval $[0,1]$ with initial condition $f(x)=x$ and boundary conditions $u_x(0,t)=0$ and $u(1,t)=0$?
(a)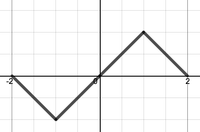 . . (b)
. . (b) 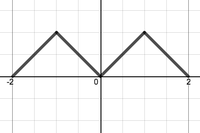
(c)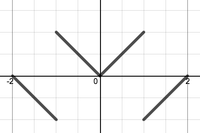 . . (d)
. . (d) 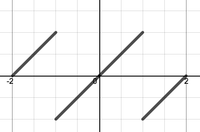
- You add 5 grams of salt per minute through the left end ($x=0$) of a 3m pipe filled with water. The salt diffuses in the pipe with diffusion coefficient $D=2$ m$^2/$min. The right end of the pipe ($x=3$) is connected to an extremely large tank that starts with no salt in it. What is the steady state concentration profile through the pipe?
- $c_{ss}(x) = \frac{5}{2}x-\frac{15}{2}$
- $c_{ss}(x) = -\frac{2}{5}x$
- $c_{ss}(x) = -\frac{2}{5}x+\frac{6}{5}$
- $c_{ss}(x) = -\frac{5}{2}x+\frac{15}{2}$
- Choose the best option for a guess at the particular solution to the equation $y'''+2y'' = t + e^{-2t}$.
- $ y_p(t)=At+B+Cte^{-2t}$
- $ y_p(t)=At^2+Bt+Cte^{-2t}$
- $ y_p(t)=At^2+Bt+Ce^{-2t}$
- $ y_p(t)=At^3+Bt^2+Cte^{-2t}$
- Books are taken out of a library at a constant rate. Books are returned to the library at a rate proportional to how many books are currently checked out from the library. On the 8th day of the semester, a large delivery of new books arrives at the library. Choose the best model for the number of books in the library $B(t)$ at time $t$ measured in days from the start of the semester.
- $\frac{dB}{dt} = r(B_0-B) - c + a\delta(t-8)$
- $\frac{dB}{dt} = r(B_0-B) - c + au_8(t)$
- $\frac{dB}{dt} = c - rB + a\delta(t-8)$
- $\frac{dB}{dt} = c - rB + au_8(t)$
- Match the general solution to the vector field
- $\mathbf{y}(t) = c_1 e^{8t}\begin{pmatrix} 1 \\ 1 \end{pmatrix}+c_2 e^{4t}\begin{pmatrix} 1 \\ -1 \end{pmatrix}$
- $\mathbf{y}(t) = c_1 e^{8t}\begin{pmatrix} 1 \\ 1 \end{pmatrix}+c_2 e^{-4t}\begin{pmatrix} 1 \\ -1 \end{pmatrix}$
- (i) -- A; (ii) -- B.
- (i) -- C; (ii) -- B.
- (i) -- A; (ii) -- D.
- (i) -- C; (ii) -- D.