Difference between revisions of "Tutorial Week 5"
From UBCMATH WIKI
(→Worksheet Questions, February 6, 2017) |
(→Worksheet Questions, February 6, 2017) |
||
| Line 14: | Line 14: | ||
## For what values of $\alpha$ (i) are both eigenvalues postive, (ii) are both eigenvalues negative, (iii) do the eigenvalues have opposite sign, (iv) is one eigenvalue zero? | ## For what values of $\alpha$ (i) are both eigenvalues postive, (ii) are both eigenvalues negative, (iii) do the eigenvalues have opposite sign, (iv) is one eigenvalue zero? | ||
## Sketch the eigenvectors and some solution curves of the system $\mathbf{x'} = A\mathbf{x}$ in the case when $\alpha = 0$. | ## Sketch the eigenvectors and some solution curves of the system $\mathbf{x'} = A\mathbf{x}$ in the case when $\alpha = 0$. | ||
| + | |||
| + | ===Solutions:=== | ||
| + | |||
| + | <ol> | ||
| + | <li> '''8pts total''' | ||
| + | <ol> | ||
| + | <li>'''2 pts''' for form (constant coefficient linear system with inhomogeneous terms), '''2 pts''' for the details of the terms (A, B) so total '''6 pts'''. | ||
| + | \begin{equation} | ||
| + | \begin{pmatrix} | ||
| + | A'(t) \\ B'(t) | ||
| + | \end{pmatrix}= | ||
| + | \begin{pmatrix} | ||
| + | -b/V & c/V \\ | ||
| + | b/V & -(a + c)/V | ||
| + | \end{pmatrix} | ||
| + | \begin{pmatrix} | ||
| + | A(t) \\ B(t) | ||
| + | \end{pmatrix} | ||
| + | + | ||
| + | \begin{pmatrix} | ||
| + | K a \\ 0 | ||
| + | \end{pmatrix} | ||
| + | \end{equation} </li> | ||
| + | <li> '''2pts''' By using $b = a + c$, eigenvalues are ('''1pt''') $\frac{-b \pm \sqrt{bc}}{V}.$ Since $b \ge 0$ and $c \ge 0$ these are real ('''1pt''' - must be explained). </li> | ||
| + | </ol> | ||
| + | |||
| + | <li>'''14pts total''' | ||
| + | <ol> | ||
| + | <li> '''6pts''' Eigenvalues are $3\alpha \pm 6$ ('''2pts''') with corresponding eigenvectors ('''4pts''') $e_1 = \begin{pmatrix}1\\2\end{pmatrix}$ and $e_2 = \begin{pmatrix}7\\2\end{pmatrix}.$ | ||
| + | </li> | ||
| + | <li> '''4pts - one for each category''' There is a zero eigenvalue for $\alpha = \pm 2$, the eigenvalues are both negative for $\alpha < -2$, the eigenvalues are both positive for $\alpha > 2$, the eigenvalues have mixed signs for $-2 < \alpha < 2$.</li> | ||
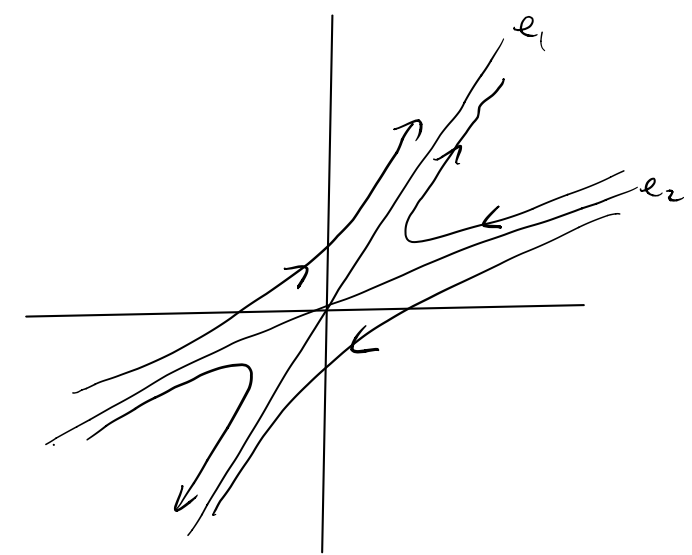
| + | <li> '''4pts''' Sketch of eigenvectors from (a) worth '''2pts''' and sketch of solution curves as below '''2pts'''. | ||
| + | [[File:52cPhasePlotSketch.png]] | ||
| + | </li> | ||
| + | </ol> | ||
| + | </li> | ||
| + | </ol> | ||
Revision as of 18:07, 9 March 2017
Worksheet Questions, February 6, 2017
You can print the PDF.
- Salt water with concentration of $K$ in g/L flows into Tank A at a rate $a$ in L/min. The mixed solution in Tank A flows into Tank B at a rate $b$ L/min. Another pipe takes the solution in Tank B back into Tank A at a rate $c$ in L/min. Finally, solution drains out of Tank B at a rate $a$ in L/min. Note: the initial volume $V$ in each tank is the same and $a + c = b$ (to ensure that the volumes in the tanks are constant).
- Write down the system in matrix form that gives the amount of salt in each tank (call these $A(t)$ and $B(t)$) at any given time.
- Show that the eigenvalues of the matrix for this system are real, and therefore it is impossible for this system to have oscillations (damped or otherwise). \textit{Hint}: express the matrix in terms of $b$ and $c$ only. Optional: show that both eigenvalues are negative.
- Consider the matrix $A = \left(\begin{array}{cc}
3\alpha - 8 & 7 \\
-4 & 3\alpha + 8
\end{array}\right).$
- Find the eigenvalues and eigenvectors of $A$.
- For what values of $\alpha$ (i) are both eigenvalues postive, (ii) are both eigenvalues negative, (iii) do the eigenvalues have opposite sign, (iv) is one eigenvalue zero?
- Sketch the eigenvectors and some solution curves of the system $\mathbf{x'} = A\mathbf{x}$ in the case when $\alpha = 0$.
Solutions:
- 8pts total
- 2 pts for form (constant coefficient linear system with inhomogeneous terms), 2 pts for the details of the terms (A, B) so total 6 pts. \begin{equation} \begin{pmatrix} A'(t) \\ B'(t) \end{pmatrix}= \begin{pmatrix} -b/V & c/V \\ b/V & -(a + c)/V \end{pmatrix} \begin{pmatrix} A(t) \\ B(t) \end{pmatrix} + \begin{pmatrix} K a \\ 0 \end{pmatrix} \end{equation}
- 2pts By using $b = a + c$, eigenvalues are (1pt) $\frac{-b \pm \sqrt{bc}}{V}.$ Since $b \ge 0$ and $c \ge 0$ these are real (1pt - must be explained).
- 14pts total
- 6pts Eigenvalues are $3\alpha \pm 6$ (2pts) with corresponding eigenvectors (4pts) $e_1 = \begin{pmatrix}1\\2\end{pmatrix}$ and $e_2 = \begin{pmatrix}7\\2\end{pmatrix}.$
- 4pts - one for each category There is a zero eigenvalue for $\alpha = \pm 2$, the eigenvalues are both negative for $\alpha < -2$, the eigenvalues are both positive for $\alpha > 2$, the eigenvalues have mixed signs for $-2 < \alpha < 2$.
- 4pts Sketch of eigenvectors from (a) worth 2pts and sketch of solution curves as below 2pts.