Difference between revisions of "Practice problems/A photographer at the skatepark"
From UBCMATH WIKI
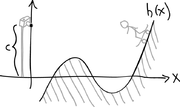
(Created page with "<caption>'''Figure 1'''. The shape of the half-pipe, <math>h(x)</math>, with camera at height <math>c</math>.</caption> A photographer is taking p...") |
|||
| Line 2: | Line 2: | ||
A photographer is taking pictures at a skatepark. The [[Wikipedia:Half-pipe|"half-pipe"]] has the shape of a function given by | A photographer is taking pictures at a skatepark. The [[Wikipedia:Half-pipe|"half-pipe"]] has the shape of a function given by | ||
:<math>h(x)=x^3-6x+11x-6</math> | :<math>h(x)=x^3-6x+11x-6</math> | ||
| − | where <math>x</math> is the horizontal distance from the photographer and <math>h(x)</math> is the height of the half-pipe surface above the point <math>x</math> (see Figure 1), both measured in tens of meters. The photographer has his camera mounted on a tall rod. He would like to hold the camera at a | + | where <math>x</math> is the horizontal distance from the photographer and <math>h(x)</math> is the height of the half-pipe surface above the point <math>x</math> (see Figure 1), both measured in tens of meters. The photographer has his camera mounted on a tall rod. He would like to hold the camera at a height <math>c</math> that is high enough so that there is no part of the half-pipe hidden from view. What is the minimum value of <math>c</math> for which this will be the case? |
[This problem is a bit tricky.] | [This problem is a bit tricky.] | ||
Revision as of 14:13, 2 September 2013
A photographer is taking pictures at a skatepark. The "half-pipe" has the shape of a function given by h(x)=x3−6x+11x−6 where x is the horizontal distance from the photographer and h(x) is the height of the half-pipe surface above the point x (see Figure 1), both measured in tens of meters. The photographer has his camera mounted on a tall rod. He would like to hold the camera at a height c that is high enough so that there is no part of the half-pipe hidden from view. What is the minimum value of c for which this will be the case?
[This problem is a bit tricky.]